Fast 3D-vector matrix transformation using SSE4

In this blog-post we'd like to show how to efficiently transform multiple 3D vectors using an affine transformation matrix. Each vector has three coordinates (x, y and z) and the matrix consists of three rows each with 4 elements (3 for rotation/scale + 1 for translation). In order to multiply a 3-element vector with a 3x4 matrix, we add an additional 1 at the end of the 3D vector:

Intel Architecture Code Analyzer

Intel provides a great tool for static code analysis of C++ code at assembly-code-level. It is called the Intel Architecture Code Analyzer and will allow you to analyze how instructions are executed on an Intel CPU (including instruction pairing and the critical path).

Bilinear Pixel Interpolation using SSE

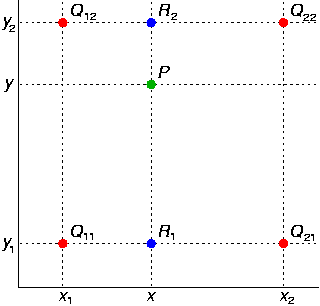Bilinear pixel interpolation is a common operation in image processing applications (resizing, distorting, etc.) as well as in computer graphics (texturing, etc.). It allows accessing pixels at non-integer coordinates of the underlying image by building a weighted sum over all neighbors of the specified image position. On GPUs this operation is implemented in hardware. However, some algorithms can not be ported to the GPU easily and a CPU implementation of the Bilinear interpolation is needed.

This article will show how to efficiently implement such an operation in C++ using SSE2 instructions for 8-bit RGBA images. First, we will show how to perform bilinear interpolation using pure C++ code and then present an enhanced example where we utilize SSE intrinsics.

How to process a STL vector using SSE code

In C++ it's very convenient to store array data using the std::vector from the STL library. On modern CPUs you can take advantage of vectorized instructions that allow you to operate on multiple data elements at the same time. But how do you combine a std::vector with SSE code? For example, you want to sum up each element of a float vector of arbitrary length (in C++ this corresponds to std::accumulate(v.begin(), v.end(), 0.0f)). This article will show you how to access the elements of the vector using SSE intrinsics and accumulate all elements into a single value.

3D Point Projection to 2D Image Using SSE

The most common operation in 3D applications is to project 3D points to a 2D image, most often that is your computer screen. For that purpose you normally use your graphics card which is most efficient at this task. But there are times, when you need to further process 2D points on your CPU. This article will show you how to efficiently perform 3D point projection in C++ using SSE intrinsics.

Loading four consecutive 3D vectors into SSE registers

In the previous two post, we showed you how to load one or two three-element float vectors using SSE intrinsics and a combination of 128-bit, 64-bit and 32-bit loads. When loading 4 3D vectors that are tightly packed in memory, we need to load 12 float values in total, which is possible using only three 128-bit load operations. In order to perform mathematical operations with them, it's practical to have one vector per register. The following code shows you how to load 12 float values and distributes them to four SSE registers, so that each register contains a X, Y and Z value (the fourth component is unused).

Vector Cross Product using SSE Code

A common operation for two 3D vectors is the cross product:

|a.x|   |b.x|   | a.y * b.z - a.z * b.y |
|a.y| X |b.y| = | a.z * b.x - a.x * b.z |
|a.z|   |b.z|   | a.x * b.y - a.y * b.x |

Executing this operation using scalar instructions requires 6 multiplications and three subtractions. When using vectorized SSE code, the same operation can be performed using 2 multiplications, one subtraction and 4 shuffle operations: